Channel pruning for CNN

Deploying vision models to embedded system has a lot of constraints, e.g. inference speed, memory consumption. These constraints are often not imposed during the training time. In addition, it's often that different people are in charge of model training and model deployment. Therefore, it's important to be able to optimize the model speed or memory consumption after training. In this post, I will go over the paper "Channel Pruning for Accelerating Very Deep Neural Networks", and discuss some techniques to improve model inference speed.

Overview

This paper focuses on structural simplification of a neural network. There are three main categories discussed in the paper, namely tensor factorization, sparse connection and channel pruning.

• Tensor factorization tries to decompose the weight tensor into smaller ones, which can further reduce the number of multiplication.
• Sparse connection push small weights to 0 to reduce computation. If the sparsity is not sufficient where dense tensor multiplcation is still used, the speed up is very limited.
• Channel pruning tries to remove less important channels, that leads to less computation. However, the challenge lies in how to minimize the accuracy drop after removing the channel.

Channel Pruning by LASSO regression

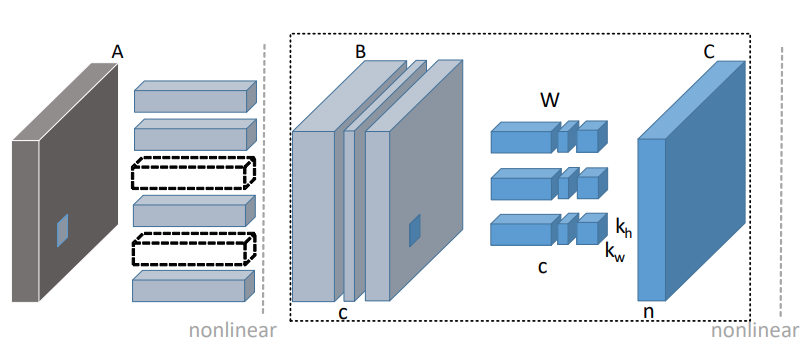
Problem formulation

Assuming we have convolution filters with shape $n * c * k_h * k_w$, where $n$ is the output channel size, $c$ is the input channel size and the kernel size is $k_h$ and $k_w$. To prune the filters, N input volumes are sampled from this feature map, where we will get a batch of feature map with size $N * c * k_h * k_w$. It will produce an output matrix $Y$ with shape $N * n$.

The optimization problem can be formulated as

$argmin_{\beta,W}{ \frac{1}{2N} \lVert{Y-\sum_{i=1}^{c}{\beta_i X_i W_i^T}}\lVert^2_F + \lambda * \lVert \beta \lVert_1}$

subject to $\lVert \beta \lVert_{0} <= c, \lVert W_i \lVert_F=1$

When I was reading the paper, there are two questions in my mind:

1. How to sample input volumes from feature map? It actually requires a data set to extract feature map. The pruning performance depends on how the data set is constructed, but it was not mentioned explicitly in the paper.

2. Why we need to add a constraint of $\lVert W_i \lVert_F=1$ and when there would be a trivial solution. It's not well explained in the paper. My guess is that the contraint is added to avoid getting the original weight.

Solving optimization

After formulating the optimization problem, solving it requires two iterative steps, where the first step solves for $\beta_i$ to reduce channels and the second step solves for $W_i$ to minimize reconstruction error.

Finally, the paper also mentioned this technique can be used for whole model pruning and handle multi-branch network.

Summary

Reducing matrix computation is the key towards improving model inference speed. It's mentioned that with both channel pruning and tensor factorization, the inference speed of VGG16 can be speeded up 4 times. This method is also provided by Tencent's model compression framework PocketFlow.