Monoid and Segment Tree

Recently, I start to learn Scala. As previously trained as an object-oriented programmer，I was not very comfortable with the functional way of thinking. After reading more materials, I start to appreciate the beauty of funtional programming. The way towards abstraction in functional programming enables me to view programming in another way. In this article, I would like to share my attempt to use the concept of Monoid for Segment Tree implementation. This idea is inspired by a zhihu answer posted by Bolyn Su and Scala tutorials written by hongjiang.

Monoid

From Wikipedia, we can find out the definition of Monoid, which is just an algebraic structure with associative binary operation and an identity element. By referring to hongjiang's code, a Monoid can be represented by the following Scala code, with a property zero (identity element abstracted out from addition's identity element) and a function add (represents the associative binary operation).

trait Monoid[T] {
  def zero: T
  def add(a: T, b: T): T
}

object Monoid {
  implicit val IntMonoid = new Monoid[Int] {
    def add(a: Int, b: Int) = a + b
    def zero = 0
  }

  implicit val StringMonoid = new Monoid[String] {
    def add(a: String, b: String) = a + b
    def zero = ""
  }
}

Segment Tree

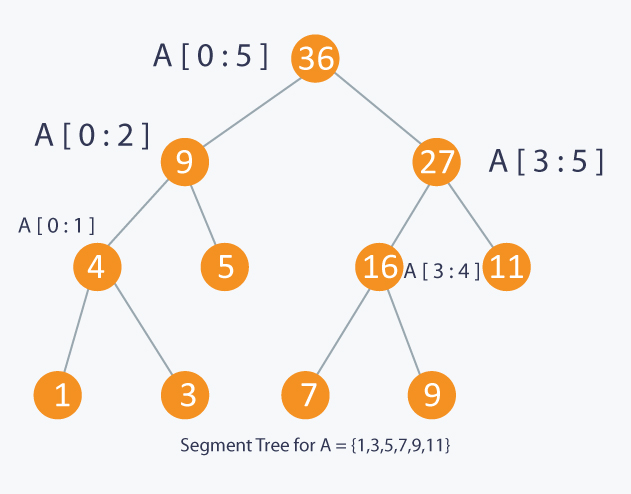
A segment tree is a data structure enabling us to query and update partial sum quickly. The speed-up is achieved by recursively computing partial sum of the left half elements and the right half elements in an array. By using such struture, updating an element does not require us to re-compute all the partial sums. As a result, segment tree has query and update complexity as $o(log n)$ . A detailed description can be found here.

However, this is not the end of the story. If we extend the concept of partial sum as $\sum_{i=m}^{n} {e_i} = e_{m} * e_{m+1} * ... * e_{n}$ , where $*$ is the associative binary operation. Futhermore, we can define an Identity element $I \rightarrow I * e_i = e_i * I = e_i$ . We might notice that segment tree can be applied to quickly query and update partial sum of any Monoid.

Scala Implementation

In the previous two sections, the concept of Monoid and Segment Tree is introduced. We also notice the partial sum in Segment Tree can be abstracted out to any Monoid. In this section, I would love to share my implement of segment tree in Scala. First of all, let us defined an abstract class for tree nodes. The tree node should contain left/right children, left/right indices for the array range, and finally the partial sum.

abstract class SegmentTreeNode[T] {
  var leftChild: SegmentTreeNode[T]
  var rightChild: SegmentTreeNode[T]
  var leftIdx: Int
  var rightIdx: Int
  var partialSum: T
}

After implementing the tree node, we can set-up a basic structure for the segment tree with Monoid initialized

class SegmentTree[T: Monoid] (arr: Array[T]) {
  // SegmentTree should work for any Monoid
  val m = implicitly[Monoid[T]]
  var root = buildTree(arr, 0, arr.length-1)

  def findMiddleIdx(lIdx: Int, rIdx: Int): Int = {
    val mIdx: Int = (lIdx + rIdx) / 2
    return mIdx
  }
}

Once we have the segment tree structure ready, we can start implementing the function that builds the segment tree, as shown below:

def buildTree(arr: Array[T],
            lIdx: Int,
            rIdx: Int): SegmentTreeNode[T] = {
    if (lIdx == rIdx) {
          // leave nodes
        var node = new SegmentTreeNode[T] {
          var leftIdx = lIdx
          var rightIdx = rIdx
          var leftChild = null.asInstanceOf[SegmentTreeNode[T]]
          var rightChild = null.asInstanceOf[SegmentTreeNode[T]]
          var partialSum = arr(lIdx)
        }
        return node
    } else {
        // recursively build tree
        val mIdx: Int = findMiddleIdx(lIdx, rIdx)
        var node = new SegmentTreeNode[T] {
          var leftIdx = lIdx
          var rightIdx = rIdx
          var leftChild = buildTree(arr, lIdx, mIdx)
          var rightChild = buildTree(arr, mIdx+1, rIdx)
          var partialSum = m.zero
        }
        node.partialSum = m.add(node.leftChild.partialSum,
                                node.rightChild.partialSum)
        return node
    }
}

Then we can continue with the function that computes the partial sum

  def getSum(node: SegmentTreeNode[T], l: Int, r: Int): T = {
    // Abstract partial sum
    if (node.leftIdx >= l && node.rightIdx <= r) {
      return node.partialSum
    } else if (node.rightIdx < l || node.leftIdx > r) {
      return m.zero
    } else {
      return m.add(getSum(node.leftChild, l, r),
                   getSum(node.rightChild, l, r))
    }
  }

Next, if an element is modified, we want to update the necessary partial sums, so we also need an update method.

  def update(node: SegmentTreeNode[T],
             idx: Int,
             value: T): Unit = {
    if((node.leftIdx == idx) && (node.rightIdx == idx)) {
      node.partialSum = value
    } else if (node.leftIdx > idx || node.rightIdx < idx) {
      // skip
    } else {
      // propogate updated partialSum from leaves
      val mIdx: Int = findMiddleIdx(node.leftIdx, node.rightIdx)
      if(idx > mIdx) {
        update(node.rightChild, idx, value)
      } else {
        update(node.leftChild, idx, value)
      }

      node.partialSum = m.add(node.leftChild.partialSum,
                              node.rightChild.partialSum)
    }
  }
}

Finally, we could add some test cases to verify the implementation.

object TestSegmentTree {
  def main(args: Array[String]): Unit = {
    // Test Integer Array
    val intArray = Array(1,4,3,2,1,1,0,5,10)
    var intSegTree = new SegmentTree(intArray)

    println(intSegTree.getSum(intSegTree.root, 1, 4)) // 10
    intSegTree.update(intSegTree.root, 3, 7)
    println(intSegTree.getSum(intSegTree.root, 1, 4)) // 15

    // Test String Array
    val strArray = Array(1,4,3,2,1,1,0,5,10)
                        .map((x: Int) => x.toString)
    var strSegTree = new SegmentTree(strArray)
    
    println(strSegTree.getSum(strSegTree.root, 1, 4)) // "4321"
    strSegTree.update(strSegTree.root, 3, "7")
    println(strSegTree.getSum(strSegTree.root, 1, 4)) // "4371"
  }
}

Now, let us ask the last question: if you want to perserve the partial max, e.g. given $m,n$ , return $max(e_m, e_{m+1}, ..., e_{n})$ , where do you need to modify in the code?

Again, we can verify that maximum operation is associative binary operation and there is an Identity element $I = -inf \rightarrow max(I, e_i) = e_i$ . Therefore, we just need to modify the Monoid definition as following:

object Monoid {
  // use Double as example
  implicit val DoubleMonoid = new Monoid[Double] {
    def add(a: Double, b: Double) = math.max(a, b)
    def zero = java.lang.Double.MIN_VALUE
  }
}

To see the full version of code, please refer to this page.